문제 설명
algospot.com :: TRAVERSAL
트리 순회 순서 변경 문제 정보 문제 트리를 순회하는 알고리즘은 트리의 모든 노드들을 특정 순서에 맞춰 방문하지만, 트리는 배열처럼 1차원적인 구조가 아니기 때문에 단 한 가지의 당연한
www.algospot.com

- 이진트리가 있다.
- 이진트리는 세 가지 방법으로 순회할 수 있다.
- 전위순회 : 루트 -> 왼쪽 서브 트리 -> 오른쪽 서브 트리
- 중위순회 : 왼쪽 서브 트리 -> 루트 -> 오른쪽 서브 트리
- 후위순회 : 왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 루트
=> 전위순회했을 때, 중위순회했을 때의 노드들의 방문 순서가 주어질 때, 후위순회했을 때의 방문 순서를 출력하기
문제 풀이
전체 트리구조 찾기가 가능할까?
처음에는 문제에서 주어지는 전위순회했을 때와 중위순회했을 때의 경우를 이용해 전체 트리 구조를 찾고, 그를 이용해 후위순회를 수행하려 했다.
하지만 이 정보를 저장할 배열의 크기를 정하려니 노드의 개수는 100개로 한정되어 있지만
트리의 깊이가 깊어질수록 인덱스의 크기는 2배로 커지기 때문에 배열의 크기도 2배수로 커져야 한다.
따라서 전체 트리구조를 찾는 것은 어려울 것 같고
전위, 중위 순회를 분석하면서 후위 순회 순서를 출력해야겠다고 생각했다.
전위순회의 특징 활용하기
전위순회를 통한 노드의 방문 순서의 특징으로는 루트 노드가 가장 먼저 나온다는 점이다.
그 후로는 루트 노드 기준 왼쪽 서브 트리 묶음과 오른쪽 서브 트리 묶음을 방문한다.

하지만 전위 순회에서는 어디까지가 왼쪽 트리의 끝인지
즉, 오른쪽 트리가 언제 시작되는지 알 수 없다.
중위순회의 특징 활용하기
중위순회에서는 루트 노드의 위치만 알면, 그를 기준으로 왼쪽트리, 오른쪽 트리를 구분할 수 있다.
하지만 중위순회만으로는 루트 노드의 위치를 알 수 없다.
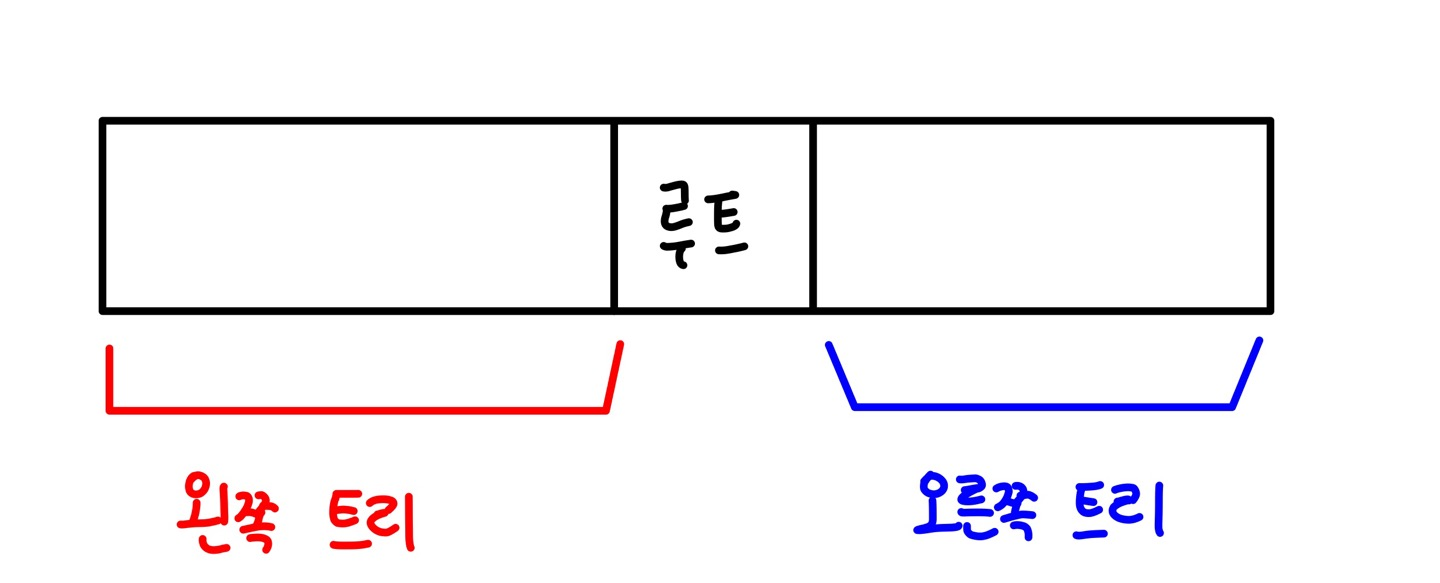
두 순회의 특징 활용하기
두 순회의 특징을 통해 전위순회로는 루트 노드의 위치를, 중위순회로는 왼쪽 트리와 오른쪽 트리를 알 수 있다.
후위 순회는 왼쪽 트리 -> 오른쪽 트리 -> 루트 순서로 방문하므로
전위순회, 중위순회를 통해 알아낸 정보로 재귀방식을 이용해 후위순회 순서대로 탐색 후 출력하면 답을 구할 수 있다.
문제 풀이 코드
#include <iostream>
using namespace std;
// 루트 n, 왼쪽서브 2*n, 오른쪽 서브 2*n+1
// 전위순회 : n -> 2*n -> 2*n+1
// 중위순회 : 2*n -> n -> 2*n+1
// 후위순회 : 2*n -> 2*n+1 -> n
// 전체 트리 구조를 구하기에는 한줄로(예, 오른쪽 자식으로만 이어지는 경우 등) 트리가 이루어질때
// 리프노드의 인덱스가 몇까지 커질지 예측할 수 없음
// 따라서 탐색과정에서 후위순회를 수행해야 함
int preorder[100];
int inorder[100];
int preorderIndex[1001];
int inorderIndex[1001];
int solve(int preIndex, int inStartIndex, int inEndIndex) {
if (inStartIndex == inEndIndex) {
cout << preorder[preIndex] << " " ; // 더 탐색할 자식노드가 없을 때
return 1;
}
else if (inStartIndex > inEndIndex) { // 범위를 벗어날 때(더 출력할 노드가 없을 때)
return 0;
}
int preNum = preorder[preIndex]; // 전위순회 루트노드 찾기
int inIndex = inorderIndex[preNum]; // 중위순회에서의 루트노드 위치 찾기
int leftCnt = solve(preIndex + 1, inStartIndex, inIndex - 1); // 루트노드 기준 왼쪽트리 탐색
int rightCnt = solve(preIndex + leftCnt + 1, inIndex + 1, inEndIndex); // 루트노드 기준 오른쪽트리 탐색
cout << preorder[preIndex] << " "; // 루트노드 출력
return leftCnt + rightCnt + 1; // 탐색한 노드 개수 반환
}
int main() {
int C;
cin >> C;
for (int tc = 1; tc <= C; ++tc) {
int N;
cin >> N;
for (int i = 0; i < N; ++i) {
cin >> preorder[i];
preorderIndex[preorder[i]] = i;
}
for (int i = 0; i < N; ++i) {
cin >> inorder[i];
inorderIndex[inorder[i]] = i;
}
solve(0, 0, N - 1);
}
return 0;
}
'알고리즘 문제풀이 > 알고리즘 문제해결전략' 카테고리의 다른 글
| 23.3_변화하는 중간값_RUNNINGMEDIAN (0) | 2023.07.21 |
|---|---|
| 21.5_요새_FORTRESS (0) | 2023.06.06 |
| 19.6_외계 신호 분석_ITES (2) | 2023.05.10 |
| 19.4_짝이 맞지 않는 괄호_BRACKETS2 (0) | 2023.05.03 |
| 18.5_조세푸스 문제_JOSEPHUS (0) | 2023.04.25 |