Treejin's Note

문제 설명

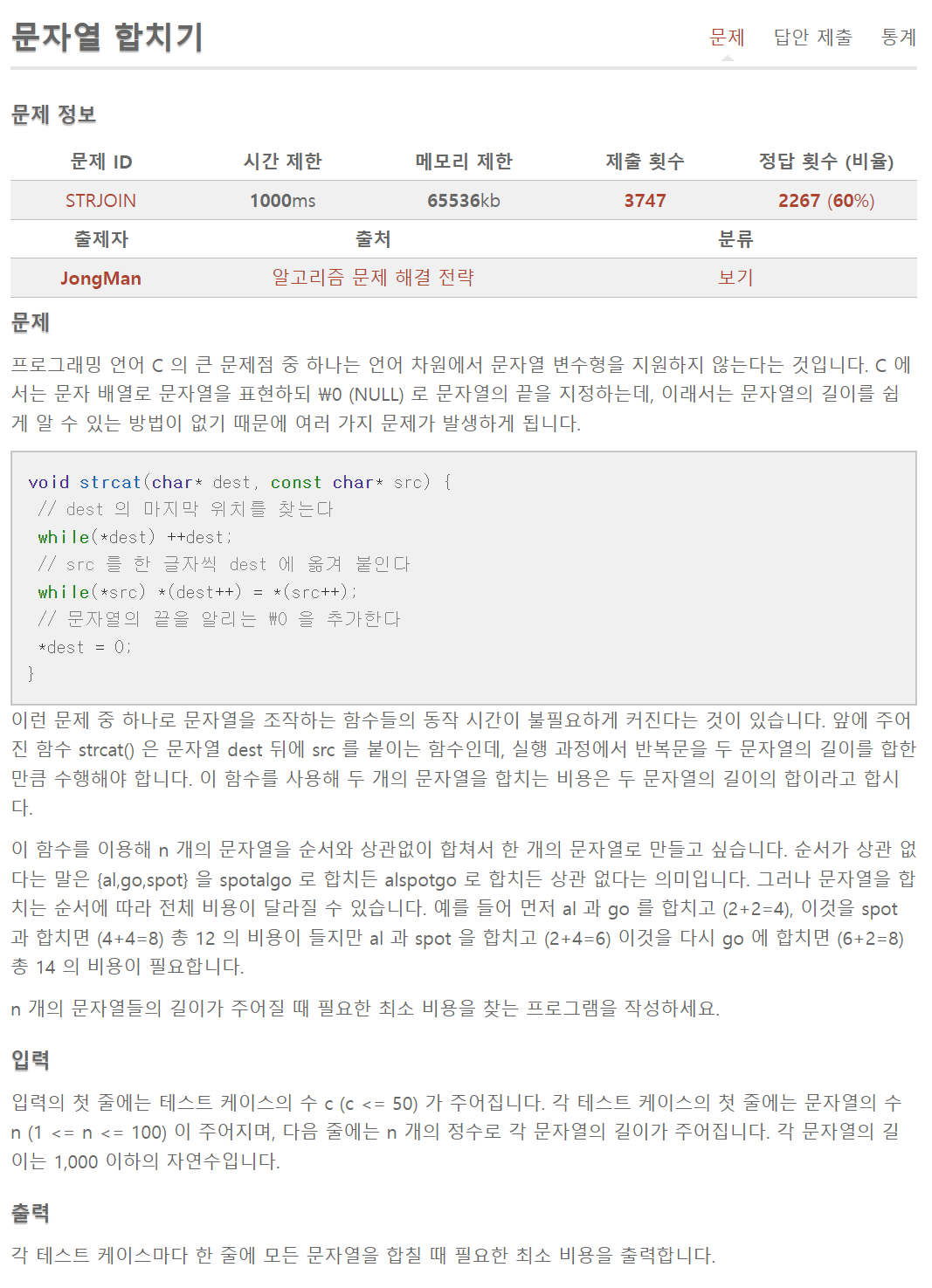
• 두 개의 문자열을 합치는 비용 = 두 문자열 길이의 합
• 문자열을 합치는 순서에 따라 전체 비용이 달라진다.
• (2+2) + (2+2+4) = 12
• (2+4) + (2+4+2) = 14

=> n개의 문자열들의 길이가 주어질 때 필요한 최소 비용을 출력하기

문제 풀이

문자열을 합치는 최소비용이란

예시에서 주어진 문자열의 계산법은

(a+b) + (a+b+c) + ... 으로 이루어진다.

먼저 더해진 문자열들은 뒤의 연산에 계속 사용되므로

짧은 문자열이 먼저 더해지는 것이 이후의 연산결과를 줄일 수 있는 방법이다.

계산 과정

문자열이 더해지고 나면, 기존 문자열 2개 -> 길이가 늘어난 문자열 1개가 새로 생긴다.

이 문자열을 포함하여 가장 짧은 문자열 두개를 더해가는 과정을 반복하고

그 비용을 출력하였다.

문제 풀이 코드

#include <iostream>

using namespace std;

#define MAXN 100

int strlength[MAXN];
int temp[MAXN];

void mergeSort(int startIdx, int endIdx, int mid) {
	int i = startIdx;
	int j = mid + 1;
	int l = startIdx;

	while (i <= mid && j <= endIdx) {
		// 문자열의 길이가 짧은 것을 앞에 배치
		if (strlength[i] < strlength[j])
			temp[l++] = strlength[i++];
		else
			temp[l++] = strlength[j++];
	}

	while (i <= mid)
		temp[l++] = strlength[i++];
	while (j <= endIdx)
		temp[l++] = strlength[j++];

	for (int l = startIdx; l <= endIdx; ++l)
		strlength[l] = temp[l];
}

void sort(int startIdx, int endIdx) {	// 정렬
	if (startIdx >= endIdx) return;
	int mid = (startIdx + endIdx) / 2;

	sort(startIdx, mid);
	sort(mid + 1, endIdx);
	mergeSort(startIdx, endIdx, mid);
}

int main() {
	int C;
	cin >> C;
	for (int tc = 1; tc <= C; ++tc) {
		int n;
		cin >> n;
		for (int i = 0; i < n; ++i) {
			cin >> strlength[i];
		}

		if (n == 1) {
			cout << strlength[0] << endl;
			continue;
		}

		int sum = 0;
		int cnt = n;
		// 더해진 문자열을 포함해 가장 짧은 두 문자열을 더하기
		for (int i = 0; i < n-1; ++i) {
			sort(0, cnt - 1);
			sum += strlength[0] + strlength[1];
			strlength[0] += strlength[1];
			strlength[1] = strlength[--cnt];
		}

		cout << sum << endl;
	}
	return 0;
}

문제 설명

• n개의 도시락이 있다.(1 <= n <= 10000)
• 도시락을 데우는데 쓰는 전자레인지는 1개 뿐이다.
• 도시락을 데우는 데는 m초, 먹는데는 e초가 걸린다.
• 도시락을 먹는 시간 : 첫 번째 도시락을 데우기 시작하는 순간 ~ 마지막 사람이 도시락을 다 먹을 때까지 걸리는 시간.

=> 도시락을 먹는데 걸리는 최소 시간을 출력하기

문제 풀이

도시락을 먹는 시간을 단축하기 위해서는

도시락을 먹는 시간은 데우는 시간 m, 먹는 시간 e로 이루어진다.

도시락은 한 번에 하나만 데울 수 있다. 모든 도시락을 데우고 다 먹어야 하므로 최소 sum(m)시간은 걸릴 것이다.

그렇다면, 도시락을 전부 데운 후(sum(m))에 먹기만 하는 시간을 최소화할 수 있는 방법으로 순서를 정해야 전체 시간을 단축시킬 수 있다.

이는 곧 마지막에 남는 e가 작아야 하므로, e가 큰 것부터 먼저 먹기 시작하는 것이 전체 시간을 최소화하는 방법이다.

문제 풀이 코드

#include <iostream>

using namespace std;

#define MAXVALUE 10000
#define MAX(a, b) (a > b ? a : b)

int lunchBox[MAXVALUE][2];
int sortedIndex[MAXVALUE];
int temp[MAXVALUE];

void mergeSort(int startIdx, int endIdx, int mid) {
	int i = startIdx;
	int j = mid + 1;
	int l = startIdx;

	while (i <= mid && j <= endIdx) {
		// e가 큰 것부터 앞에 배치
		if (lunchBox[sortedIndex[i]][1] > lunchBox[sortedIndex[j]][1])
			temp[l++] = sortedIndex[i++];
		else
			temp[l++] = sortedIndex[j++];
	}

	while (i <= mid)
		temp[l++] = sortedIndex[i++];
	while (j <= endIdx)
		temp[l++] = sortedIndex[j++];

	for (int l = startIdx; l <= endIdx; ++l)
		sortedIndex[l] = temp[l];
}

void sort(int startIdx, int endIdx) {	// 정렬
	if (startIdx >= endIdx) return;
	int mid = (startIdx + endIdx) / 2;

	sort(startIdx, mid);
	sort(mid + 1, endIdx);
	mergeSort(startIdx, endIdx, mid);
}

int main() {
	int C;
	cin >> C;
	for (int tc = 1; tc <= C; ++tc) {
		int n;
		cin >> n;
		for (int i = 0; i < 2; ++i) {
			for (int j = 0; j < n; ++j) {
				cin >> lunchBox[j][i];
			}
		}
		for (int j = 0; j < n; ++j) {
			sortedIndex[j] = j;
		}

		sort(0, n - 1);
		
		int chingTime = 0;	// 데우기 시작한 시간
		int endTime = 0;	// 다 먹은 시간
		for (int i = 0; i < n; ++i) {
			chingTime += lunchBox[sortedIndex[i]][0];
			endTime = MAX(endTime, chingTime + lunchBox[sortedIndex[i]][1]);
		}

		cout << endTime << endl;
	}
	return 0;
}

문제 설명

• 두니발 박사는 검문을 피해 산길로만 이동한다.
• 두니발 박사는 교도소를 탈출한 당일, 교도소와 인접한 마을 하나로 도망쳐 은신한다.
• 두니발 박사는 이후 매일 인접한 마을로 움직여 은신한다.
• 산길(간선)과 마을(노드)가 주어진다.
• n개의 마을이 주어진다.(2 <= n <= 50)
• 탈출부터 지금까지 지난 일 수 d가 주어진다.(1 <= d <= 100)
• 교도소가 있는 마을의 번호 p가 주어진다.
• i번 마을에서 j번 마을을 잇는 산길에 대한 정보 A행렬이 주어진다.
• 확률을 계산할 마을의 번호 q가 t개 주어진다.

=> d일 후 마을 q에 두니발 박사가 있을 확률을 구하기

문제 풀이

재귀 함수 규칙 찾기

문제에 주어진 그림에서

1. 0번 마을에 첫째날 두니발 박사가 도달할 확률은 1/5이다.

1/5의 5는 교도소로 주어진 3번 마을의 간선의 개수이다.

즉, 3번 마을 -> 1번 마을로 오는 확률은 1/[3번 마을의 간선의 개수] 인것이다.

2. 0번 마을에 둘째날 두니발 박사가 도달하려면

두니발 박사가 첫째날에 0번 마을과 인접한 1, 2, 3번 마을에 있어야 둘째날 0번 마을에 도달할 수 있다.

즉, 0번 마을에 둘째날 두니발 박사가 도달할 확률은

(첫째날 1번 마을에 도달할 확률 x 1번에서 0번으로 오는 확률 ) +

(첫째날 2번 마을에 도달할 확률 x 2번에서 0번으로 오는 확률 ) + 

(첫째날 3번 마을에 도달할 확률 x 3번에서 0번으로 오는 확률 ) 

으로 구할 수 있다.

1번과 2번에서 " d번째날 n번 마을에 도달 확률"이  반복되는 것을 알 수 있다.

이를 작은 문제로 쪼개어 재귀 함수로써 풀 수 있다.

기저 조건

d번째날 n번 마을부터 시작해서 d-1번째날, d-2 번째날, ... , 첫째날 으로 내려가는데

첫째날에는 교도소로 주어진 번호 p와 연결되어 있어야 두니발 박사가 움직일 수 있는 확률이 생긴다.

메모이제이션

d번째날 n번 마을에 도달할 확률에 대해서 중복적으로 접근할 수 있기에

메모리에 d, n 과 관련된 확률 값을 저장하여 중복 연산을 방지하고 시간을 단축할 수 있다.

문제 풀이 코드

#include <iostream>
#include <string.h>

using namespace std;

int n, d, p, t;
int links[50][50];			// 간선 정보
int linkCnt[50];			// 간선 개수
double percentage[50][101];	// index, day 의 확률

double calPercentage(int index, int day) {
	double& ret = percentage[index][day];
	if (ret != -1.0)
		return ret;

	if (day == 1) {			// 첫째 날
		if (links[p][index] == 1)	// 교도소와 연결되어 있어야 확률 반환
			return (1.0 / (double)linkCnt[p]);
		return 0.0;			// 아니면 0
	}

	ret = 0;
	for (int i = 0; i < n; ++i) {
		if (links[i][index] == 1) {
			ret += ((1.0 / (double)linkCnt[i]) * calPercentage(i, day - 1));
		}
	}

	return ret;
}

int main() {
	ios_base::sync_with_stdio(false); 
	cin.tie(0);

	int C;
	cin >> C;
	for (int tc = 1; tc <= C; ++tc) {
		cin >> n >> d >> p;
		memset(linkCnt, 0, sizeof(linkCnt));
		for (int i = 0; i < n; ++i) {
			for (int j = 0; j <= d; ++j) {
				percentage[i][j] = -1.0;	// 초기화
			}
		}

		for (int i = 0; i < n; ++i) {		// 간선 입력받기
			for (int j = 0; j < n; ++j) {
				cin >> links[i][j];
				if(links[i][j] == 1)
					++linkCnt[i];
			}
		}

		cin >> t;
		for (int i = 0; i < t; ++i) {
			int num;
			cin >> num;
			calPercentage(num, d);
			cout << fixed;					// 출력 소숫점 아래 8자리로 고정
			cout.precision(8);
			cout << percentage[num][d];
			if (i != t - 1)
				cout << " ";
		}
		cout << endl;
	}
	return 0;
}

문제 설명

• 폴리오미노 : 정사각형들의 변들을 서로 완전하게 붙여 만든 도형
• 세로 단조 폴리오미노 : 어떤 가로줄도 폴리오미노를 두 번 이상 교차하지 않는 폴리오미노
• 폴리오미노를 구성하는 정사각형의 개수 n이 주어진다.(1 <= n <= 100)

=> n개의 정사각형으로 구성된 세로 단조 폴리오미노의 개수를 10,000,000으로 나누어 출력하기

문제 풀이

한 줄에 놓이는 정사각형의 개수

세로 단조 폴리오미노, 어떤 가로줄도 폴리오미노를 두 번 이상 교차하지 않으려면

가로 한 행에 놓여진 정사각형들이 모두 붙어있어야 한다는 의미이다.

따라서 한 줄에 n개, n-1개, n-2개,....,1개를 놓고

그 아래줄에 n-1개, n-2개, ... , 1개를 놓고

...

이런 식으로 진행하면 된다.

각각을 작은 문제로 쪼개면

한 줄에 놓을 수 있는 정사각형의 개수 n을 받은 후, 그중 a개를 놓고, 그 다음줄에 n-a개를 넘겨주는

재귀함수로 표현할 수 있다.

정사각형들의 위치

한 줄에 놓을 정사각형의 개수를 정했다면,

어떤 위치에 놓아야 하는지도 중요하다.

각 정사각형의 변은 붙어있어야 하므로 윗줄과 아랫줄이 완전히 분리되어서는 안된다.

윗 줄이 2칸, 아랫 줄이 3칸이라고 했을 때 배치할 수 있는 경우의 수는 다음 그림과 같다.

a + b 에 완전히 분리되는 1가지 경우를 제외한 a + b - 1의 경우의 수가 발생한다.

즉, b개의 정사각형을 배치한 후 윗줄에 놓여진 정사각형의 개수를 참고하여 연산한 값을 반환해야 한다.

메모이제이션

남은 정사각형의 개수가 같다면 놓여질 수 있는 경우의 수도 같다.

이에 대한 중복연산을 방지하기 위해 메모이제이션에 연산 결과를 저장하여 사용할 수 있다.

문제 풀이 코드

// for (int i = leftCnt; i > 0; --i) 0ms
// for(int i = 1; i <= leftCnt; ++i) 4ms

#include <iostream>
#include <string.h>

#define DIVNUM 10000000

using namespace std;

int memoization[101][101];

int makePolyomino(int top, int leftCnt) {	// top : 이전 줄에 배치된 정사각형 개수, leftCnt : 남은 정사각형 개수
	int& ret = memoization[top][leftCnt];
	if (ret != -1) {
		return ret;
	}

	if (leftCnt == 0)
		return ret = 1;

	ret = 0;
	//for(int i = 1; i <= leftCnt; ++i){
	for (int i = leftCnt; i > 0; --i) {		// i : 이번 줄에 배치할 정사각형 개수
		ret += (makePolyomino(i, leftCnt - i) * (i + top - 1)) % DIVNUM;
		ret %= DIVNUM;
	}

	return ret;	// 메모리에 담겨져 다른 경우에 활용 가능해지는 시점
}

int main() {
	int C;
	cin >> C;
	memset(memoization, -1, sizeof(memoization));
	for (int tc = 1; tc <= C; ++tc) {
		int n;
		cin >> n;
		int sum = 0;
		//for(int i = 1; i <= n; ++i){	// i : 맨 윗줄에 놓을 정사각형
		for (int i = n; i > 0; --i) {
			sum += makePolyomino(i, n - i) % DIVNUM;
		}
		cout << sum % DIVNUM << endl;
	}
	return 0;
}

참고

메모이제이션 & 재귀 호출 순서에 대한 속도 차이

문제를 풀다가 궁금한 점이 생겼다.

n, n-1, n-2, ... , 1 순서대로 배치하는 것과 1, 2, 3, ... , n 순서대로 배치하는 것에 시간차이가 발생할까?

순서를 바꾸어서 답안을 제출해본 결과,

n, n-1, n-2, ... , 1로 연산한 결과가 0ms

1, 2, 3, ... , n으로 연산한 결과가 4ms가 나왔다.

이는 메모이제이션에 저장하는 시점으로 인한 차이이다.

n이 5라고 가정할 때, n, n-1, n-2, ... , 1 방식은

(5) -> (4,1) -> (3,2) -> (3,1,1) -> (2,3) -> ... 순서로 재귀가 진행될 것이다.

이 때, 메모이제이션되는 시점은 밑줄이 쳐진 부분. 즉, 연산의 끝에 도달한 순간부터 거꾸로 진행된다.

하지만 1, 2, 3, ... , n 방식에서는

(1,1,1,1,1) -> (1,1,1,2) -> (1,1,2,1) -> (1,1,3) -> (1,2,1,1) -> ... 순서로 재귀가 진행되는데,

1,1에 대한 연산이 이미 중복되어 진행된 후에 메모리에 담기므로

중복연산을 줄여주는 메모이제이션의 역할이 많이 발휘되지 못한다.

따라서 메모리에 담기는 시점을 고려하여 재귀 순서를 결정하는 것도

시간 단축에 있어 도움이 된다는 것을 배웠다!

문제 설명

• 타일링 : 2 * n 크기의 직사각형을 2 * 1 또는 1 * 2 (90도 회전) 크기의 직사각형으로 채우기(1 <= n <= 100)
• 대칭 타일링 : 채워진 직사각형의 모양이 좌우 대칭인 경우
• 비대칭 타일링 : 채워진 직사각형의 모양이 좌우 비대칭인 경우

=> 비대칭 타일링의 수를 1,000,000,007로 나눈 나머지를 출력하기

문제 풀이

1. 전체 타일링 개수 구하기

우선, 타일링을 하는 방법으로는

• 세로 직사각형(1*2) 한 개 채우기
• 가로 직사각형(2*1) 두 개 위 아래로 채우기

로 분류할 수 있다.

  1번의 경우는 가로 1칸이 채워지고

  2번의 경우는 가로 2칸이 채워진다.

경우의 수를 따져보면,

   n=1 -> 세로 직사각형 1개

   n=2 -> 가로 직사각형 2개, 세로 직사각형 1 + 1개

   n=3 -> 가로 직사각형 2 + 세로 직사각형 1개, 세로 직사각형 1 + 1 + 세로 직사각형 1개, 세로 직사각형 1개 + 가로 직사각형 2개

으로 확인할 수 있는데,

n = 3의 경우에서, (n=2의 경우 * 세로 직사각형 1개를 붙이기) + (n=1의 경우 * 가로 직사각형 2개를 붙이기)임을 알 수 있다.

따라서 f(n) = f(n-2) + f(n-1) 으로 전체 타일링의 개수를 구할 수 있다.

2. 대칭 타일링 개수 구하기

문제에서 요구하는건 비대칭 타일링인데

비대칭 타일링에 대한 규칙은 찾을 수 없지만 대칭 타일링은 직접 만들어낼 수 있다.

만약 n=8인 직사각형을 채운다고 할 때,

n=4인 직사각형을 양쪽으로 데칼코마니처럼 찍어내면 대칭 타일링을 구할 수 있다.

n이 짝수일 때 대칭 타일링을 만들어내는 방법은 두 가지가 있다.

• 정확히 2등분 하기
• 가운데 가로 직사각형 2개를 걸치기

첫 번째의 경우는 n/2의 경우를 구하면 되지만,

가운데에 가로 직사각형 2개가 걸쳐진다면 절반에서 1칸을 더 사용하므로 (n/2 - 1)의 경우를 구해야 한다.

n이 홀수일 때 대칭 타일링을 만들어내는 방법은 한 가지이다.

• 가운데 세로 직사각형 1개를 두기

이 경우에는 n/2의 경우를 구하면 된다.

3. 비대칭 타일링 개수 구하기

위와 같은 방식으로 구해진 전체 타일링 개수와 대칭 타일링 개수를 활용하여

   비대칭 타일링 개수 = 전체 타일링 개수 - 대칭 타일링 개수

값을 구할 수 있다.

계산 과정에서 메모이제이션을 활용하여

이미 연산한 n개의 직사각형에 대하여 중복연산 하지 않도록 시간을 단축시켰다.

문제 풀이 코드

/*
	비대칭의 개수 = 전체 개수 - 대칭의 개수
	전체 개수 = n-2의 개수 + n-1의 개수
	대칭의 개수 = n % 2 == 0 ? (n/2의 개수 + n/2 - 1의 개수) : n/2의 개수
*/

#include <iostream>
#include <string.h>

#define DIVNUM 1000000007

int memoization[101];

using namespace std;

int getTilingCount(int num) {
	int& ret = memoization[num];
	if (ret != -1)
		return ret;
	return ret = ((getTilingCount(num - 1) + getTilingCount(num - 2)) % DIVNUM);
}

int main() {
	int C;
	cin >> C; 

	memset(memoization, -1, sizeof(int) * 101);
	memoization[0] = 0;
	memoization[1] = 1;
	memoization[2] = 2;

	for (int tc = 1; tc <= C; ++tc) {
		int n;
		cin >> n;
		// 전체 타일링 개수 구하기
		int totalCnt = getTilingCount(n);
		// 대칭 타일링 개수 구하기
		int symCnt = n % 2 == 0 ? getTilingCount(n / 2 + 1) : getTilingCount(n / 2);
		int result = totalCnt - symCnt;
		cout << (result < 0 ? result + DIVNUM : result) << endl;
	}
	return 0;
}