문제 설명
algospot.com :: KAKURO2
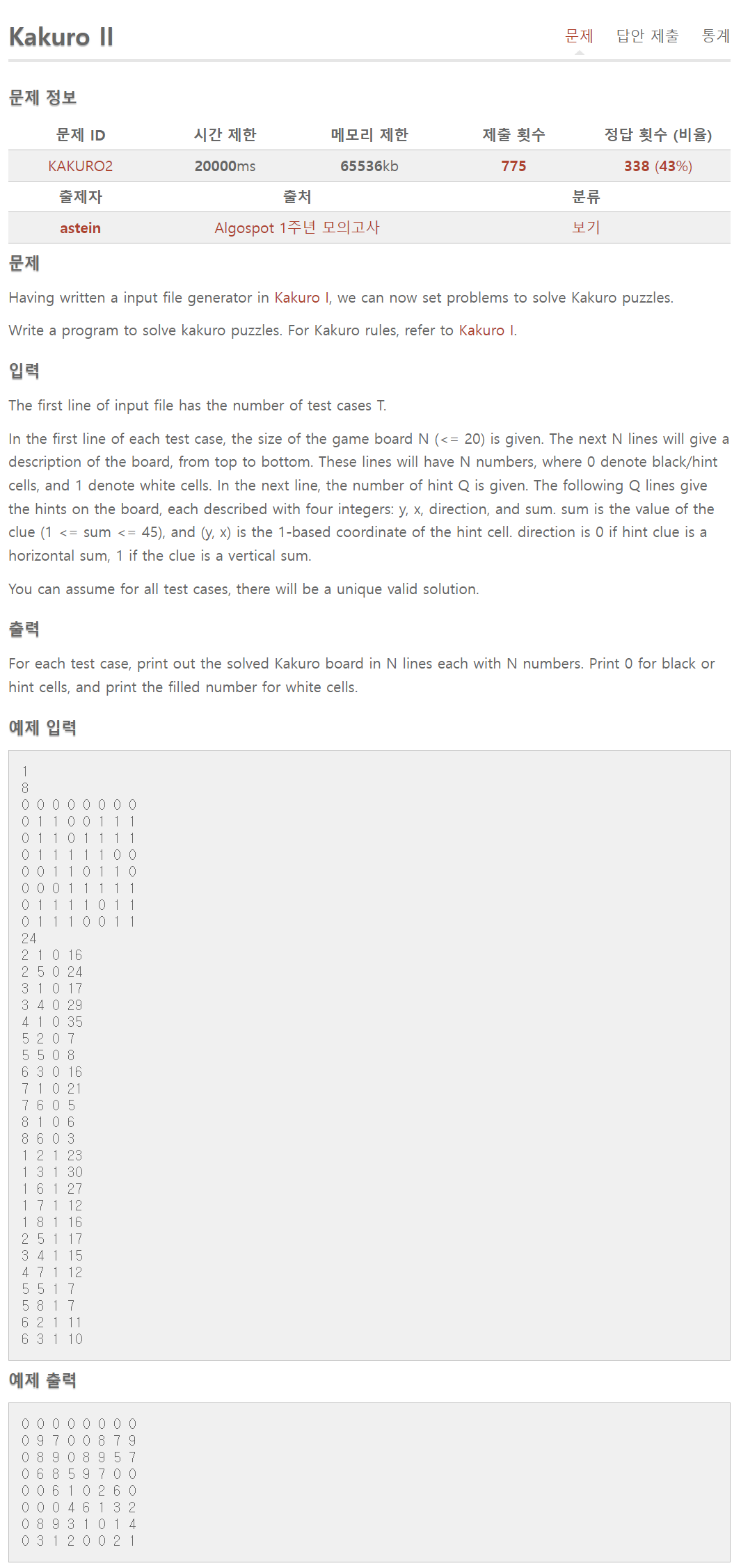
Kakuro II 문제 정보 문제 Having written a input file generator in Kakuro I, we can now set problems to solve Kakuro puzzles. Write a program to solve kakuro puzzles. For Kakuro rules, refer to Kakuro I. 입력 The first line of input file has the num
www.algospot.com
- 게임판의 각 칸은 흰 칸, 검은 칸, 또는 힌트 칸 중 하나이다.
- 흰 칸에 적절히 숫자를 채워 다음 규칙을 만족시킨다.
- 모든 흰 칸에는 1~9의 정수가 들어간다.
- 세로로 연속한 흰 칸의 수를 모두 더하면, 그 칸의 바로 위에 있는 힌트 칸의 왼쪽 아래에 적힌 숫자가 나와야 한다.
- 가로로 연속한 흰 칸의 수를 모두 더하면, 그 칸의 바로 왼쪽에 있는 힌트 칸의 오른쪽 위에 적힌 숫자가 나와야 한다.
- 이 때, 한 줄을 이루는 연속된 흰 칸들에는 같은 수를 두 번 넣을 수 없다.
- 테스트 케이스 C(C <= 50), 게임판의 크기 N(1 <= N <= 20), 검은 칸은 0, 흰 칸은 1, 힌트의 수 Q, 힌트의 정보 y, x(1 <= y, x <= N), direction(0: 가로, 1 : 세로), sum으로 주어진다.
- 모든 테스트케이스에는 정확히 하나의 정답이 있다.
=> 각 테스트 케이스마다 n줄에 각 n개의 숫자로 모두 채워진 게임판을 출력하기. 검은 칸이나 힌트 칸은 0
문제 풀이
이 문제는 각 흰 칸을 방문하면서, 그 칸에 들어갈 수 있는 숫자의 경우의 수를 찾아 배치하는 문제이다.
흰 칸 방문 -> 가로 힌트, 세로 힌트 찾기 -> 두 힌트로 넣을 수 있는 공통된 숫자 찾기 -> 배치하기 -> 다음 흰칸 찾기
크게 위와 같은 순서로 진행이 되고, 만약 어느 순간 넣을 수 있는 값을 찾지 못하면
이전의 흰 칸으로 돌아가서 숫자를 바꾼 후 다시 진행한다.(재귀)
이 과정에서 시간을 줄일 수 있는 곳은 아래 두 가지에서 가능하다.
- 가로 힌트, 세로 힌트 찾기
- 두 힌트로 넣을 수 있는 공통된 숫자 찾기
가로 힌트, 세로 힌트 찾기
한 칸을 방문할 때마다 왼쪽으로, 위쪽으로 탐색을 하면 시간이 많이 소요되기 때문에
leftHintBoard, topHintBoard라는 배열을 만들어 각 위치에 힌트 배열의 index값을 저장하도록 했다.
두 힌트로 넣을 수 있는 공통된 숫자 찾기
각 칸에 들어갈 수 있는 수는 다음과 같다.
- 1~9인 수
- 가로, 세로 힌트의 영향을 받는 칸의 개수로 가로 힌트의 합 값을 만들 수 있는 조합에 해당하는 수
- 가로, 세로 힌트에 따른 조합 중 사용하지 않은 수
넣을 수 있는 수는 1~9까지의 수 이므로 비트마스킹을 이용해 충분히 저장 가능하다.
그러니, 2번과 3번에 해당하는 경우의 수를 배열로 미리 만들어 저장해두면
추가적인 탐색 과정 없이 바로 그 칸에 넣을 수 있는 수의 목록을 구할 수 있다.
cases[10][46][1024] 배열로
힌트의 영향을 받는 칸의 수, 힌트의 합, 사용된 숫자 목록에 따라 그 칸에 넣을 수 있는 목록을 저장하도록 만들었다.
문제 풀이 코드
#include <iostream>
#include <string.h>
using namespace std;
#define MIN(a, b)(a < b ? a : b);
#define MAX(a, b)(a > b ? a : b);
struct hint {
int sum, usedNum, cnt; // 합, 사용된 숫자, 힌트를 활용하는 수의 개수
};
bool findAnswer;
int N, Q;
int board[20][20];
int leftHintBoard[20][20];
int topHintBoard[20][20];
int answerBoard[20][20];
hint hints[400];
int cases[10][46][1 << 10]; // 영향을 미치는 칸 수, sum, 사용된 숫자
void solve(int pos) {
if (findAnswer)
return;
int r = pos / N;
int c = pos % N;
if (r == N) { // board 끝
for (int i = 0; i < N; ++i) {
for (int j = 0; j < N; ++j) {
cout << answerBoard[i][j] << " ";
}
cout << endl;
}
findAnswer = true;
return;
}
if (board[r][c]) { // 흰 칸일 때
hint& leftHint = hints[leftHintBoard[r][c]];
hint& topHint = hints[topHintBoard[r][c]];
int leftUsableNum = cases[leftHint.cnt][leftHint.sum][leftHint.usedNum];
int topUsableNum = cases[topHint.cnt][topHint.sum][topHint.usedNum];
int usableNum = leftUsableNum & topUsableNum;
if (usableNum == 0) return;
for (int i = 1; i <= 9; ++i) {
if (usableNum & (1 << i)) {
leftHint.usedNum |= (1 << i);
topHint.usedNum |= (1 << i);
answerBoard[r][c] = i;
solve(pos + 1);
leftHint.usedNum ^= (1 << i);
topHint.usedNum ^= (1 << i);
}
}
}
else solve(pos + 1);
}
void fillHintBoard() {
for (int i = 1; i < N; ++i) {
for (int j = 1; j < N; ++j) {
if (board[i][j]) { // 흰 칸
leftHintBoard[i][j] = leftHintBoard[i][j - 1];
++hints[leftHintBoard[i][j]].cnt;
topHintBoard[i][j] = topHintBoard[i - 1][j];
++hints[topHintBoard[i][j]].cnt;
}
}
}
}
int getSize(int set) { // 1의 개수 세기
int size = 0;
for (int i = 1; i <= 9; ++i) {
if (set & (1 << i))
++size;
}
return size;
}
int getSum(int set) { // 합 반환
int sum = 0;
for (int i = 1; i <= 9; ++i) {
if (set & (1 << i))
sum += i;
}
return sum;
}
void calHintCases() {
memset(cases, 0, sizeof(cases));
for (int set = 0; set < 1024; set += 2) { // 1 << 0 == 1, 1 << 1 == 2 니까, 2씩 올려야 0을 고려하지 않고 셀 수 있음.
int l = getSize(set);
int s = getSum(set);
int usedNum = set;
while (true) {
// l칸의 합이 s이고, 이 칸에 이미 쓰인 숫자의 집합이 usedNum일 때,
// 나머지 칸에 넣을 수 있는 숫자의 집합을 저장하기
// 전체 숫자의 집합이 set이 되도록 나머지 숫자 집어넣기
cases[l][s][usedNum] |= (set & ~usedNum); // 나머지 칸에 넣을 수 있는 숫자의 집합( (& ~usedNum) : 이미 사용한 숫자 제외)
if (usedNum == 0) break; // 이미 쓰인 숫자가 없으면(끝)
usedNum = (usedNum - 1) & set; // set의 부분집합 찾기
}
}
}
int main() {
int C;
cin >> C;
calHintCases();
for (int tc = 1; tc <= C; ++tc) {
findAnswer = false;
memset(board, 0, sizeof(board));
memset(leftHintBoard, -1, sizeof(leftHintBoard));
memset(topHintBoard, -1, sizeof(topHintBoard));
memset(answerBoard, 0, sizeof(answerBoard));
cin >> N;
for (int i = 0; i < N; ++i) {
for (int j = 0; j < N; ++j) {
cin >> board[i][j]; // 0 : 검은 칸, 힌트 칸 , 1 : 흰 칸
}
}
cin >> Q;
for (int i = 0; i < Q; ++i) {
int y, x, dir, sum;
cin >> y >> x >> dir >> sum;
if (dir) // hintBoard에 힌트 index 저장
topHintBoard[y - 1][x - 1] = i;
else
leftHintBoard[y - 1][x - 1] = i;
hint h = { sum, 0, 0};
hints[i] = h;
}
fillHintBoard();
solve(0);
}
return 0;
}
'알고리즘 문제풀이 > 알고리즘 문제해결전략' 카테고리의 다른 글
| 12.4_캐나다 여행_CANADATRIP (0) | 2023.04.06 |
|---|---|
| 13.3_승률올리기_RATIO (0) | 2023.04.04 |
| 12.2_남극 기지_ARCTIC (0) | 2023.03.21 |
| 11.5_알러지가 심한 친구들_ALLERGY (0) | 2023.03.11 |
| (오답)11.3_게임판 덮기2_BOARDCOVER2 (0) | 2023.03.09 |